C++ vs C# 형태 비교
| C++ 컨테이너 형태 | C# 컬렉션 형태 | 핵심 자료구조 (동일) | 특징 (동일) |
| map set |
SortedDictionary<TKey, TValue> SortedSet<T> |
레드-블랙 트리 | 자동 정렬 성능 |
| unordered_map unordered_set |
Dictionary<TKey, TValue> HashSet<T> |
해시 테이블 | 비정렬 평균 O(1)의 빠른 성능 |
※ 아래에서부터는 C++ 기준으로 설명하도록 하겠다.
연관 VS 비정렬 연관 비교
| 구분 | 연관 컨테이너 (map, set) | 비정렬 연관 컨테이너 (unordered_map, unordered_set) |
| 핵심 자료구조 | 레드-블랙 트리 (Red-Black Tree) | 해시 테이블 (Hash Table) |
| 데이터 정렬 | 키(Key) 기준으로 자동 정렬됨 | 정렬되지 않음 |
| 시간 복잡도 | 검색, 삽입, 삭제 모두 | 평균적으로 , 최악의 경우 |
| 주요 장점 | 데이터가 항상 정렬되어 있고, 성능이 안정적임 | 압도적으로 빠른 평균 속도 |
| 주요 단점 | unordered 계열보다 상대적으로 느림 | 메모리 사용량이 더 많고, 순서가 없음 |
컨테이너의 3가지 분류
컨테이너는 데이터를 저장하고 관리하는 방식을 기준으로 크게 세 가지로 나뉩니다.
- 시퀀스 컨테이너 (Sequence Containers) : 데이터를 순차적으로 저장합니다. vector, list, deque 등이 여기에 속하며, 데이터가 들어온 순서대로 정렬됩니다.
- 연관 컨테이너 (Associative Containers) : 키(Key)를 기반으로 데이터를 저장하고, 키에 따라 자동으로 정렬됩니다. map, set, multimap, multiset이 해당됩니다.
- 비정렬 연관 컨테이너 (Unordered Associative Containers) : 키(Key)를 기반으로 저장하지만, 정렬되지 않습니다. unordered_map, unordered_set 등이 속하며, 성능에 초점을 맞춘 컨테이너입니다.
이 중에서 연관 컨테이너와 비정렬 연관 컨테이너가 각각 레드-블랙 트리와 해시 테이블을 핵심 자료구조로 사용합니다.
연관 컨테이너와 레드-블랙 트리
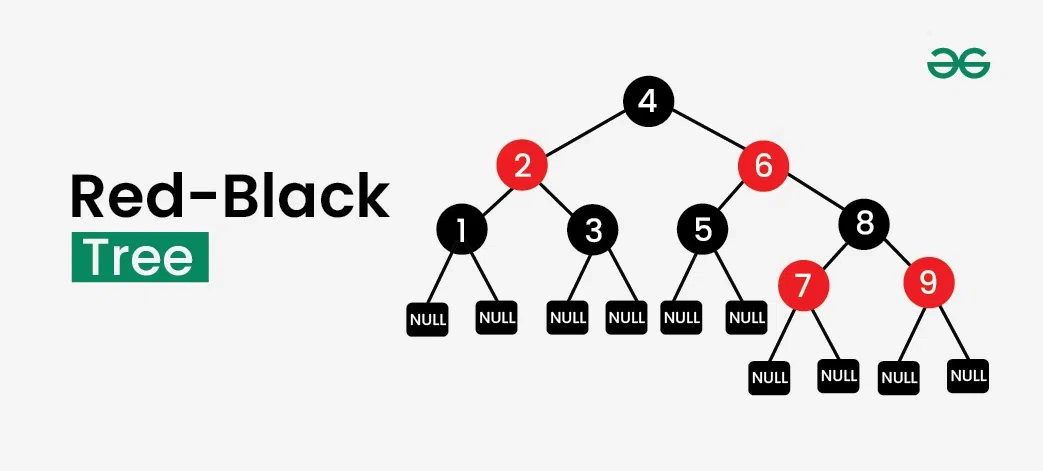
연관 컨테이너(map, set 등)는 내부적으로 레드-블랙 트리라는 자료구조를 사용합니다.
- 레드-블랙 트리(Red-Black Tree)란?
- 스스로 균형을 맞추는 이진 탐색 트리(Binary Search Tree)의 한 종류입니다.
- 노드에 '레드' 또는 '블랙'이라는 색상을 부여하는 규칙을 통해 트리의 한쪽이 너무 깊어지는 것을 방지하고, 전체적인 균형을 유지합니다.
- 특징:
- 자동 정렬 : 데이터를 삽입할 때 키의 크기를 비교하여 항상 정렬된 상태를 유지합니다. 이 때문에 map이나 set의 원소를 순회하면 키 순서대로 출력됩니다.
- 균형 잡힌 성능 : 트리의 높이가 항상 (N은 원소의 개수)에 가깝게 유지되므로 검색, 삽입, 삭제 연산이 모두 O(log N)의 시간 복잡도를 보장합니다. 데이터가 많아져도 성능 저하가 완만합니다.
- 결론 : 정렬된 상태를 유지하면서 안정적인 성능이 필요할 때 연관 컨테이너(map, set)를 사용합니다.
레드-블랙 트리의 '자가 균형' 원리
일반적인 이진 탐색 트리의 가장 큰 약점은 데이터가 순서대로 들어올 경우, 트리가 한쪽으로만 길게 늘어져 사실상 연결 리스트(Linked List)처럼 변해버리는 것입니다. 이렇게 되면 탐색 성능이 최악의 경우 O(N)까지 떨어집니다.
레드-블랙 트리는 이런 상황을 막기 위해 몇 가지 '절대 규칙'을 가지고 있습니다. 이 규칙들 덕분에 트리가 스스로 균형을 잡을 수 있습니다.
핵심 규칙 요약:
- 모든 노드는 레드 아니면 블랙이다.
- 루트 노드(가장 위)는 항상 블랙이다.
- 레드 노드는 연속으로 나올 수 없다. (즉, 레드 노드의 자식은 반드시 블랙이다)
- (※ 가장 중요) 어떤 노드에서부터 그 자손인 리프 노드(끝 노드)까지 가는 모든 경로에는 동일한 개수의 블랙 노드가 있다.
바로 4번 규칙이 트리의 균형을 유지하는 핵심입니다. 모든 경로의 '블랙 노드' 개수가 같아야 하므로, 어떤 한쪽 경로만 유독 길어지는 것을 원천적으로 방지합니다.
그렇다면 어떻게 균형을 맞출까?
새로운 데이터를 삽입하거나 삭제할 때 위의 규칙이 깨질 수 있습니다. 이때 레드-블랙 트리는 스스로 "복구 작업"에 들어갑니다. 복구 작업은 두 가지 방식으로 이루어집니다.
- 색상 변경 (Recoloring) : 규칙을 위반했을 때, 주변 노드들(삼촌, 할아버지 노드 등)의 색상을 바꾸는 간단한 작업입니다. 이것만으로 균형이 맞춰지기도 합니다.
- 회전 (Rotation) : 색상 변경만으로 해결이 안 될 때, 트리의 구조를 직접 바꾸는 작업입니다. 특정 노드를 축으로 삼아 트리의 일부를 회전시켜 높이를 맞춥니다.
이러한 규칙과 복구 작업 덕분에, 레드-블랙 트리는 높이가 항상 에 가깝게 유지되며, O(log N)의 안정적인 성능을 보장할 수 있는 것입니다.
비정렬 연관 컨테이너와 해시 테이블
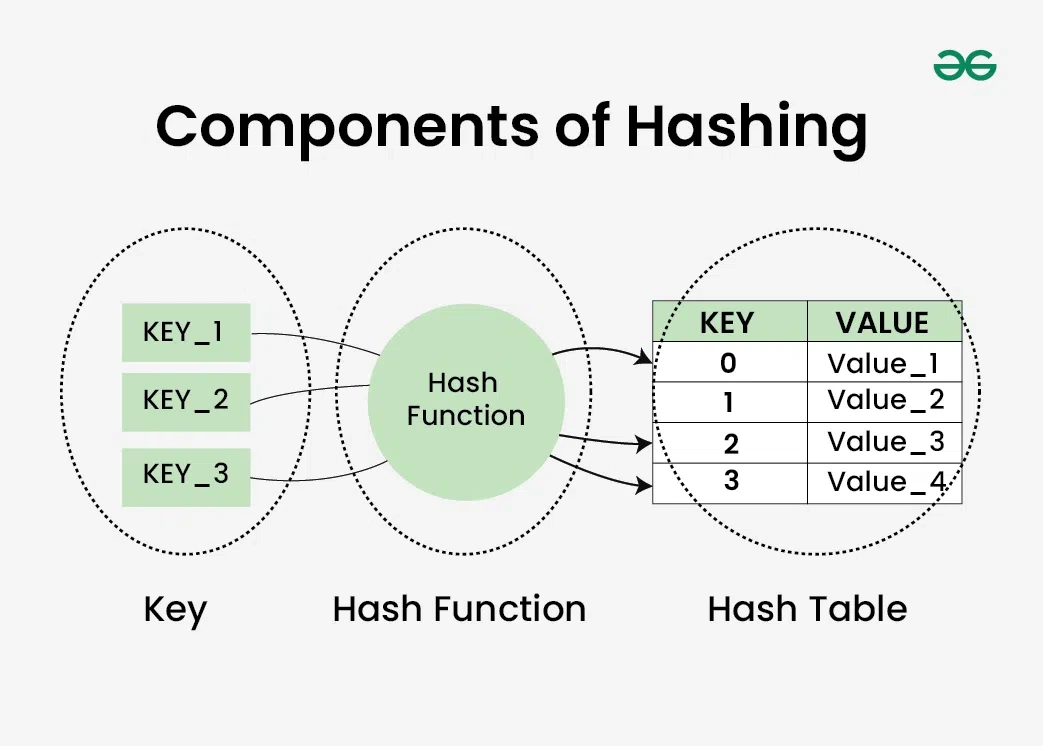
비정렬 연관 컨테이너(unordered_map, unordered_set 등)는 해시 테이블을 기반으로 만들어집니다.
- 해시 테이블(Hash Table)이란?
- 해시 함수(Hash Function)를 사용하여 키를 특정 숫자(해시 값)로 변환하고, 이 숫자를 배열의 인덱스로 사용하여 데이터에 바로 접근하는 방식입니다.
- 여러 키가 같은 인덱스를 가리키는 '해시 충돌(Hash Collision)'이 발생할 수 있으며, C++에서는 보통 각 인덱스(버킷, bucket)에 연결 리스트(Linked List)를 두어 충돌된 데이터들을 저장하는 방식으로 해결합니다.
- 특징:
- 정렬되지 않음 : 해시 함수 결과에 따라 데이터가 저장되므로 특정 순서를 보장하지 않습니다. 원소를 순회해도 예측할 수 없는 순서로 출력됩니다.
- 매우 빠른 평균 성능 : 키를 통해 해시 값만 계산하면 데이터 위치에 거의 바로 접근할 수 있습니다. 따라서 검색, 삽입, 삭제 연산의 평균 시간 복잡도가 로 매우 빠릅니다.
- 최악의 경우 : 해시 충돌이 한 인덱스에 집중되면 성능이 O(N)까지 저하될 수 있지만, 좋은 해시 함수를 사용하면 이런 경우는 드뭅니다.
- 결론 : 데이터의 순서는 중요하지 않고, 최대한 빠른 검색, 삽입, 삭제가 필요할 때 비정렬 연관 컨테이너(unordered_map, unordered_set)를 사용합니다.
해시 테이블의 '최악의 경우'와 해시 충돌
- 이상적인 상황 : 해시 테이블은 '해시 함수'를 이용해 "Apple" -> 3, "Banana" -> 5 와 같이 각 데이터를 고유한 배열 인덱스로 바꿔서 저장합니다. 그래서 데이터를 찾을 때, 해시 함수 한 번만 돌리면 데이터가 어디 있는지 바로 알 수 있죠. 이것이 O(1)의 원리입니다.
- 문제 상황 : 해시 충돌 (Hash Collision) 그런데 만약 새로운 데이터 "Cherry"를 넣으려고 보니, 해시 함수가 또 3이라는 결과를 돌려주면 어떻게 될까요? "Apple"이 이미 3번 인덱스를 차지하고 있는데 말이죠. 이것을 해시 충돌이라고 합니다.
- 해결책과 최악의 경우 : 가장 일반적인 해결책은 각 인덱스를 연결 리스트(Linked List)로 만드는 것입니다.
- 3번 인덱스에는 "Apple"이 저장되어 있습니다.
- 충돌이 발생한 "Cherry"는 "Apple" 뒤에 연결됩니다. (3 -> "Apple" -> "Cherry")
- 만약 "Durian"도 3으로 해시되면, "Cherry" 뒤에 또 연결됩니다. (3 -> "Apple" -> "Cherry" -> "Durian")
최악의 경우란, 운이 나쁘거나 해시 함수가 매우 좋지 않아서 모든 데이터가 전부 같은 인덱스로만 충돌하는 상황을 말합니다. 예를 들어 1,000개의 데이터가 모두 3번 인덱스로만 충돌한다면, 해시 테이블의 3번 인덱스에는 1,000개의 데이터를 가진 거대한 연결 리스트 하나만 덜렁 달려있는 모습이 됩니다. 이 상태에서 특정 데이터를 찾으려면 결국 이 리스트를 처음부터 끝까지 하나씩 다 뒤져봐야 합니다.
이것이 바로 선형 탐색(Linear Search)이며, 시간 복잡도는 O(N)이 됩니다. 해시 테이블의 장점인 O(1)이 완전히 사라지고, 그냥 연결 리스트와 다를 바 없게 되는 것이다.
"좋은 해시 함수"란 바로 이런 상황을 막아주는 함수입니다. 좋은 해시 함수는 데이터를 최대한 넓고 균일하게 여러 인덱스로 분산시켜서 충돌 자체를 최소화하고, 한 곳에 데이터가 몰리는 현상을 방지합니다. (그래서 실제로는 최악의 경우가 거의 발생하지 않는다.)
'CS > 자료구조' 카테고리의 다른 글
| 자료구조 (0) | 2025.10.17 |
|---|---|
| Map / Set 비교 (0) | 2025.10.16 |
| map / unordered_map (0) | 2025.10.15 |